Word Search II: One of LeetCode's Trickiest Problems Explained

Tony Montemuro

September 1st, 2025

Word Search II is a hard LeetCode problem that many people struggle to understand, let alone solve. While it may seem very difficult at first, after reading this post, my hope is that you will walk away understanding this tricky problem!

Visualizing this problem

Before I hop into the explaination, I have a tool that might help you, especially for you visial learners out there. I built a visualization tool that allows you to walk through the algorithm at any pace you like. My suggestion would be to move through the algorithm one step at a time using the “Step” control button to build up your understanding, but feel free to let the algorithm automatically play out as well!

Understanding the original Word Search problem

To really get a feel for Word Search II, you should really solve Word Search first. This problem is essentially the same as Word Search II, except you only have 1 word to worry about. If that word is contained in the board of characters, true is returned. Otherwise, return false. If you can solve this problem, you only need to worry about the problem of multiple words when attempting Word Search II, rather than also needing to worry about how to tackle traversal.

So, let’s follow my advice, and start with Word Search!

Word Search problem description:

Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example 1:

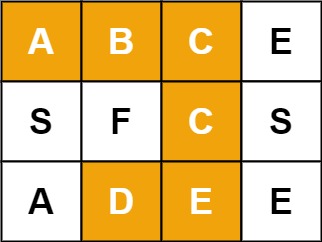
Input: board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED” Output: true

Example 2:

Input: board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCB” Output: false

Constraints:

• m == board.length
• n = board[i].length
• 1 <= m, n <= 6
• 1 <= word.length <= 15
• board and word consists of only lowercase and uppercase English letter

A naive approach

The first thing you might naturally think of is this:

• Go through the board, and check all valid arrangements of words.length characters. If we happen to find a match, we return true. Otherwise, return false.

The follow up question might be: how do we generate all valid these arrangements?

Well, let’s think of the board of characters as a graph. We could use a graph-traversal algorithm to find valid arrangements of length words.length! For example, we could use Depth-first search (DFS) to traverse the board. Here is some pseudo-code for this solution:

If you are having a hard-time understanding this pseudo-code, I suggest solving some simpler graph problems that utilize DFS first, such as Maximum Depth of a Binary Tree, or Path Sum.

However, those of you with a keen eye may notice the major inefficity of this approach: we are forced to run this expensive depth-first search for ALL characters. This is clearly unnecessary, if you just consider this example:

• Target Word: foo
• Character at [x, y]: s

Despite being obvious to us that exploring arrangements starting with ‘s’ could never possibly produce the word ‘foo’, our algorithm is not wise enough to prune this search-space. Thus, the trick to getting an efficient solution is clever pruning.

The solution

Our naive approach is actually pretty close! With just a few modifications, we can solve this problem efficiently!

As you can see in the above, instead of building out each possible arrangement of words.length, and checking for equality once our built word hits the same length, we are checking for equality at every step of the algorithm, by keeping track of the depth of the path at each step! For most inputs, this will dramatically reduce the number of recursive calls, greatly increasing the efficiency of the algorithm!

Complexity

Time complexity: O(m*n*4^(len(word)))

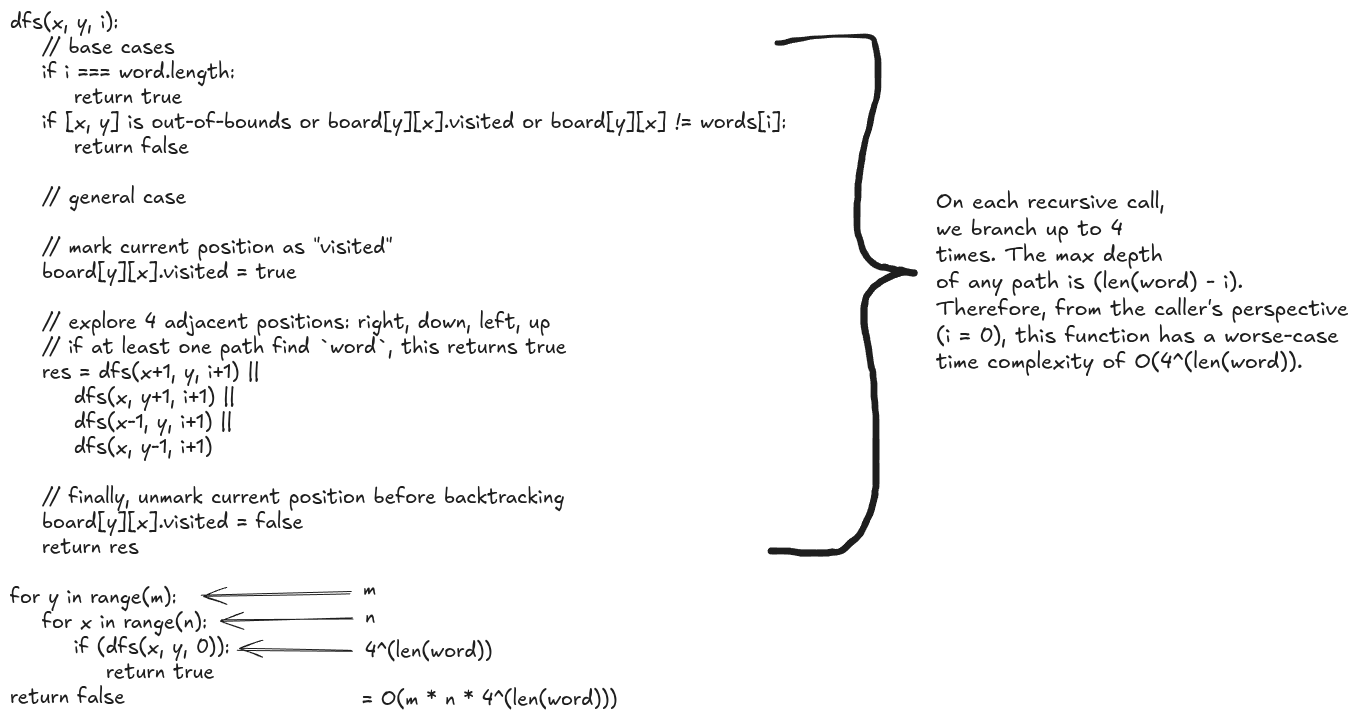
Fun fact: this is actually the same time complexity as our naive solution! However, this implementation will perform much better for almost all inputs, due to the introduced pruning. This is why, while it’s important to understand Big-O notation, there is more to algorithm performance than just Big-O!

Space complexity: This will depend on implementation. However, if you are clever with how you keep track of “visited” spaces, the space complexity becomes the maximum depth of the search, which is O(len(word)), as we need this amount of memory to maintain the call stack.

Implementation

The following is my implementation, written in JavaScript:

/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */
var exist = function(board, word) {
    const [m, n] = [board.length, board[0].length];

    function dfs(x, y, i) {
        if (i === word.length) {
            return true;
        }
        if (x < 0 || y < 0 || y === board.length || x === board[y].length || board[y][x] !== word[i]) {
            return false;
        }
        
        // maintain a backup of current value at position [x, y], and
        // use special character '#' to mark as visited. we can safely do this,
        // since problem constraints states that board and word consists of
        // letters only
        const c = board[y][x];
        board[y][x] = '#';

        const res = dfs(x+1, y, i+1) ||
            dfs(x-1, y, i+1) ||
            dfs(x, y+1, i+1) ||
            dfs(x, y-1, i+1);

        // unvisit [x, y], and backtrack
        board[y][x] = c;
        return res;
    }

    for (let y = 0; y < m; y++) {
        for (let x = 0; x < n; x++) {
            if (dfs(x, y, 0)) {
                return true;
            }
        }
    }

    return false;
};

Returning to Word Search II

Whoo! That was probably a lot! However, if you made it this far, and you deeply understand Word Search, Word Seach II is not too bad! Let’s look at the problem description of Word Search II, to see what is new.

Problem description

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:

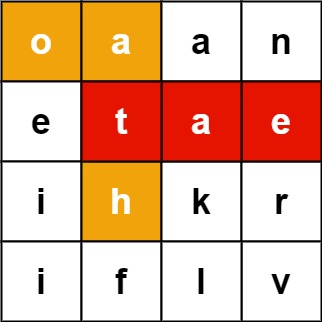
Input: board = [[“o”,“a”,“a”,“n”],[“e”,“t”,“a”,“e”],[“i”,“h”,“k”,“r”],[“i”,“f”,“l”,“v”]], words = [“oath”,“pea”,“eat”,“rain”]

Output: [“eat”,“oath”]

Example 2:

Input: board = [[“a”,“b”],[“c”,“d”]], words = [“abcb”]

Output: []

Constraints:

• m == board.length
• n == board[i].length
• 1 <= m, n <= 12
• board[i][j] is a lowercase English letter.
• 1 <= words.length <= 3 * 10^4
• 1 <= words[i].length <= 10
• words[i] consists of lowercase English letters.
• All the strings of words are unique.

A naive approach

After understanding Word Search, the naive approach is pretty obvious. We could reuse our Word Search algorithm, and run it for each word in words. However, there are many problems with doing this:

• Word Search itself is already not a super efficient algorithm, having a Time Complexity of O(n*m*4^len(word)). We would need to execute that len(words) times.
• There is the potential to have up to 3,000 words, as described in the constraints.
• The maximum size of the board can actually be up to 4 times larger than the original questions maximum, since n / m can be as large as 12 now (up from 6).

Therefore, we need to be a bit more clever, and really think about the nature of this problem, as performance is crucial. Ideally, we need to be able to verify we are on a valid path in O(1) time. Is this even possible?! Well, yes, it is!

Tries

The trick to solving this problem is representing words as a Trie. Tries, also known as prefix trees, are a search tree data structure, which allows for efficient search, insertions, and deletion of strings.

Search: O(n)

Insertion: O(n)

Deletion: O(n)

Tries essentially break up words into single characters, where the connections between nodes represent characters. Each node specifies any proceeding connections, as well as whether or not we have reached the “end” of a word.

This data structure is often missed / underappreciated in CS curriculums, so if you are unfamiliar with this data structure, do not worry! I would suggest solving Implement Trie (Prefix Tree) before proceeding. It’s really not too complicated of a data structure once you get the hang of it (and also very cool!)

Solution

So, let’s say we represent words as a Trie. How does this help us? Well, once we have done this, we can actually use a fairly similar approach to Word Search: DFS with backtracking, with pruning for added efficiency. The only difference is how we will prune the search space. Instead of checking if the character at position [x, y] is equal to a single character in a single word, we will:

• Traverse the Trie graph alongside the board graph
• If the character at [x, y] is not a child (connection) of the current TrieNode, we know the current pathway will not generate a word, so we can return.
  • This is actually an O(1) operation, since we represent connections as a Map of characters to TrieNodes!

This allows us to traverse our board graph in a similar manner as we did before, efficiently pruning any invalid paths along the way! Here’s what the pseudo-code would look like:

You may notice this code looks quite similar to that of Word Search! It is, but there are some notable differences:

• Since we need to worry about more than one word, we necessarily have to build up the current word as we traverse the graph. We do this by adding a character before going down a layer in the graph.
• Our dfs function no longer returns a boolean value, instead returning void. This is because we are using this function to extend our global res array, which will contain the result.
• As I explained before, you can actually see how we traverse our trie alongside the board graph. Basically, if we are at a valid position in the graph, we move down the trie based on the connection associated with the character at [x, y]. If we happen to hit the end of a word, we make sure up update res, and set endOfWord to false.
  • It is very important to remember to set endOfWord to false! This prevents duplicates words in the result.

Complexity

Time complexity: O(len(words)*L + m*n*4^L) = O(m*n*4^L), where L = average length of word in words.

The len(words) * L comes from the time complexity of building our Trie. If you recall, the time complexity of inserting a string into a Trie scales linearly with the number of characters in the string. We insert len(words) words into the Trie, resulting in an O(len(words)*L) operation. However, the traversal of the graph, O(m*n*4^L) (same complexity as original Word Search)! is generally much more expensive than building the Trie, so this part of the algorithm is the limiting factor for performance.

Space complexity: O(len(words)*L) + O(L) + O(len(words)) = O(len(words)*L)

There are three significant uses of memory in this algorithm.

• O(len(words)*L) of memory for our Trie (approximately L nodes for len(words) words).
• O(L) of memory required to maintain the call stack of our DFS recusion. L is approximately the maximum depth of our search.
• O(len(words)) for the result. In the worst case, all words in the input are found in the board of words, and are added to our result.

For this problem, the most significant usage of memory is the Trie. Therefore, O(len(words)*L) is the final space complexity.

Implementation

Unfortunately, the pseudo-code compared to the implementation of Word Search II is a larger difference relative to that of Word Search. This is primarily because most programming languages (that I know of) do not have a Trie built into their standard library. Therefore, you will need to implement the Trie yourself. Fortunately, the only operation you need to worry about is Insert, which is not to complicated. There are many ways you could implement a Trie. However, I prefer to implement a Trie object, which contains a pointer to the head node, with any necessary methods, and a TrieNode class, which defines the node structure. Here is my JavaScript solution:

var TrieNode = function() {
    this.children = new Map();
    this.endOfWord = false;
}

var Trie = function() {
    this.head = new TrieNode();
}

Trie.prototype.insert = function(word) {
    let curr = this.head;

    for (const c of word) {
        let next = curr.children.get(c);
        if (!next) {
            next = new TrieNode();
            curr.children.set(c, next);
        }
        curr = next;
    }

    curr.endOfWord = true;
}

/**
 * @param {character[][]} board
 * @param {string[]} words
 * @return {string[]}
 */
var findWords = function(board, words) {
    const [m, n] = [board.length, board[0].length];
    const res = [];
    const trie = new Trie();
    for (const word of words) {
        trie.insert(word);
    }

    function dfs(x, y, node, word) {
        if (x < 0 || y < 0 || y === board.length || x === board[y].length || !node.children.get(board[y][x])) {
            return;
        }

        const c = board[y][x];
        const child = node.children.get(c);
        word += c;
        if (child.endOfWord) {
            res.push(word);
            child.endOfWord = false;
        }

        board[y][x] = '#';
        dfs(x+1, y, child, word);
        dfs(x, y+1, child, word);
        dfs(x-1, y, child, word);
        dfs(x, y-1, child, word);
        board[y][x] = c;
    }

    for (let y = 0; y < m; y++) {
        for (let x = 0; x < n; x++) {
            dfs(x, y, trie.head, '');
        }
    }

    return res;
};

If you made it this far, and are still lost, I remind you to check out my visualization tool that I made for this problem! Also, I would encourage you not to feel discouraged for struggling with this problem. This is a genuinely difficult problem, which I failed to solve on my first two tries. Keep practicing, and eventually things will start to click, I promise!